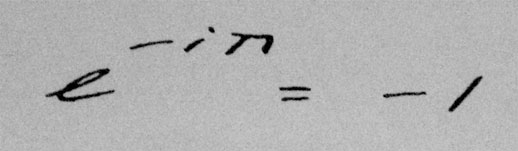
An image of Euler’s Equation, widely regarded as one of the most elegant in mathematics. Courtesy of Borkur.net
Bertrand Russell, in his book Mysticism and Logic (1918), wrote,
The first truly beautiful thing I encountered in mathematics was calculus. It was love at first sight, and I have been a mathematician ever since.
Beauty is one of the last things most calculus students associate with the subject. That’s hardly surprising. It is generally presented as a utility—a collection of techniques for solving problems to do with continuous change (in the case of differential calculus) or the computation of areas and volumes (for integral calculus). Moreover, such is the power of this toolbox, and so radically different are its techniques from anything the student has previously encountered in mathematics, that it takes the calculus novice every bit of effort and concentration simply to learn and follow the rules. Understanding those rules and knowing why they hold can come only later, if at all, and appreciation of the inner beauty of the subject later still.
Calculus was presented to me that way too, with differentiation being “just a technique” to compute the instantaneous slopes of continuous curves. But my reaction was different from most of my colleagues. Inspired by the launch of Sputnik in 1957, the year before I started high school, I was dead set on becoming a physicist and getting involved in the clearly imminent exploration of space. That was what motivated me to learn all the math I would need to become a physicist. (I was a pretty driven kid.) But then, at age 16, I met calculus. Its importance to physics was self-evident.
I quickly mastered the basic techniques of differentiation and integration, and marveled at their power. But I could not for the life of me understand how calculus worked, even less how a young man my age (Isaac Newton) had created it during a summer when his university (Cambridge) was closed because of the plague. Clearly, there was a lot more to this math stuff than I realized. I sensed that the seemingly disparate techniques that I hitherto thought was math, were just the tips of submerged mountains that, beneath the surface of the mathematical ocean, formed a solid, interconnected range.
I wanted to explore that hidden world and see what made it tick. Suddenly, physics was no longer my main goal. Instead of seeking to explore outer space, I wanted to know all there was about that hidden world of mathematics. I did not yet see its beauty. That came later, emerging gradually as I learned more about the subject. The beauty of calculus came first. Calculus is the only genuinely deep mathematics a child can encounter in a typical high school career, and hence the only part of mathematics that can really demonstrate the deep beauty Russell was referring to. But there was more to come. A lot more. Over forty years later, I still discover new beauty as I encounter and learn more mathematics.
Comments