 Chances are, you remember Erwin Schrödinger (who was born on this day 128 years ago) for his famous cat, but the high point of the celebrated physicist’s career was actually unrelated to feline thought experiments. Among scientists, he’s more renowned for giving us the fundamental tools to describe quantum behavior.
Chances are, you remember Erwin Schrödinger (who was born on this day 128 years ago) for his famous cat, but the high point of the celebrated physicist’s career was actually unrelated to feline thought experiments. Among scientists, he’s more renowned for giving us the fundamental tools to describe quantum behavior.
The 1920s, which saw the birth of quantum mechanics—the workings of the smallest, most fundamental constituents of all matter—were an exciting time to be a physicist. The greatest minds alive were rushing to find ways of describing this new world that had been cracked open. Werner Heisenberg came up with his formulation of quantum mechanics using matrices, a system that required just algebra. But Schrödinger thought of a different model using waves instead of matrices.
The wave functions of Schrödinger’s model says physicist Sean Carroll, “are more difficult to solve, but more intuitive.”
Schrödinger’s model rests on his eponymous equation, which describes the evolution of the wave function of a physical system over time. It’s kind of like a quantum version of Newton’s second law of motion (force = mass x acceleration). When describing the behavior of particles, Newton’s rules don’t work as well, so the math needs to get a little more complex. Here’s the most general form of the equation:
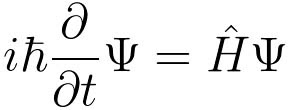 In this formula, i is the imaginary unit (the square root of -1); ħ stands for the Planck constant divided by 2π; ∂/∂t is a partial derivative changing over time; Ψ is the system’s wave function; and Ĥ is the Hamiltonian operator, which represents the energy of the system. The Hamiltonian operator is the key part: It describes the kind of system we’re looking at.
In this formula, i is the imaginary unit (the square root of -1); ħ stands for the Planck constant divided by 2π; ∂/∂t is a partial derivative changing over time; Ψ is the system’s wave function; and Ĥ is the Hamiltonian operator, which represents the energy of the system. The Hamiltonian operator is the key part: It describes the kind of system we’re looking at.
“Schrodinger’s equation lies at the very heart of theoretical physics,” says World Science Festival co-founder and Columbia University physicist Brian Greene. The equation “is not a single mathematical statement. It is a general relationship that as far as we know always holds. In any given situation, you have to know how to apply that relationship, and the details of that application do vary from situation to situation. But the law, as far as we know, is a law.”
Back to the formula’s specifics: Put it all together and, if you have a snapshot of the “wave” at one point in time, using Schrödinger’s equation allows you to talk about what it will look like in the future.
“I think of all the equations we currently know, [Schrödinger’s] is most likely to hold up 1,000 years from now,” says Carroll.
This formula was a revelation at the time. It accounts for the fact that particles don’t usually behave like little billiard balls skittering across a table; sometimes, they are better thought of as waves. While the French physicist Louis de Broglie had already conjectured that wave-particle duality existed, Schrödinger allowed scientists to describe particles—and their associated waves—in action. That was an impressive enough achievement for the scientists sitting on the Nobel Prize committee who awarded Schrödinger a Nobel Prize in Physics in 1933 (shared with fellow wave mechanics investigator Paul Dirac).
“Through a study of the wave properties of matter, [Schrödinger has] succeeded in establishing a new system of mechanics which also holds good for motion within the atoms and molecules,” H. Pleijel, then-chairman of the Nobel Committee for Physics, said in a 1933 speech presenting that year’s prizes. “Schrödinger’s wave equation has provided a convenient and simple method for handling problems to do with light spectra, and has become an indispensable tool for the present-day physicist.”
And as a coda (which is, of course, Latin for tail), let’s return quickly to the cat. While it’s not quite as indispensable a tool as Schrödinger’s equation, the “Schrödinger’s cat” thought experiment still resonates as a powerful illustration of the mercurial nature of quantum mechanics. For a refresher on just what it means, check out this video from Brian Greene.
Comments